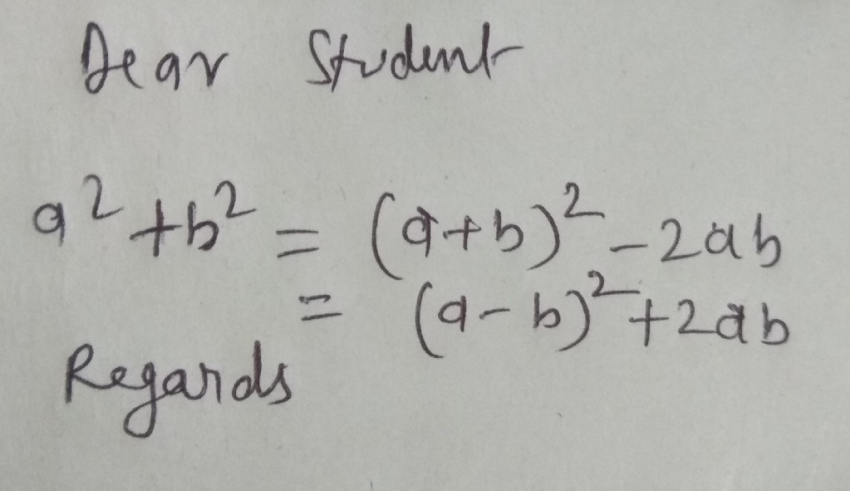
Table of Contents
Introduction:
In the realm of mathematics, few concepts have captured the imagination and curiosity of both students and scholars alike as much as the Pythagorean theorem. At the heart of this theorem lies a seemingly simple expression: a² + b². In this blog post, we embark on a journey to demystify the meaning and significance of a square + b square, exploring its origins, applications, and deeper implications in the world of mathematics.
Understanding the Pythagorean Theorem:
The Pythagorean theorem states that in a right-angled triangle, the square of the hypotenuse (the side opposite the right angle) is equal to the sum of the squares of the other two sides. Mathematically, this can be expressed as a² + b² = c², where ‘a’ and ‘b’ represent the lengths of the two shorter sides (also known as the legs), and ‘c’ represents the length of the hypotenuse.
The Power of a² + b²:
The expression a² + b² has far-reaching implications in various branches of mathematics and beyond. Let’s explore some of its key applications:
Geometry:
The Pythagorean theorem is fundamental in solving geometric problems involving right triangles. It enables us to determine unknown side lengths, identify right angles, and establish congruence between shapes. Architects, surveyors, and engineers rely on this theorem for accurate measurements and constructions.
Trigonometry:
Trigonometric functions such as sine, cosine, and tangent are based on ratios of side lengths in right triangles. By utilizing the Pythagorean theorem, we can derive these functions and develop a comprehensive understanding of angles and their relationships.
Analytical Geometry:
The concept of distance between two points in a coordinate plane relies heavily on a² + b². By applying the Pythagorean theorem, we can determine the length of the hypotenuse, which represents the distance between two points, considering their x and y coordinates.
Number Theory:
Exploring a square + b square in the realm of number theory unveils fascinating patterns. For example, any prime number greater than 2 can be expressed as the sum of two squares (a² + b²) in a unique way. This fact, known as Fermat’s theorem on sums of two squares, provides insight into the distribution of prime numbers.
a square + b square Beyond Mathematics:
The significance of a² + b² transcends the boundaries of mathematics and enters various other domains:
Physics: In physics, the Pythagorean theorem finds application in vectors, forces, and the study of motion. It serves as the foundation for the calculation of resultant vectors and the determination of net forces acting on an object.
Computer Graphics: In computer graphics, a² + b² is instrumental in calculating distances, rotations, and 3D transformations. These computations form the basis for rendering realistic images, simulating physical phenomena, and creating immersive virtual worlds.
Conclusion:
The expression a² + b², originating from the Pythagorean theorem, encompasses an array of mathematical applications and has profound implications across diverse fields. From geometry to trigonometry, from physics to computer science, this seemingly simple equation has proven to be an invaluable tool in understanding the world around us. By unraveling the mystery of a² + b², we unlock the doors to a realm of knowledge and possibilities. It not only offers practical solutions to everyday problems but also illuminates the interconnectedness of different branches of mathematics and their applications in various domains. So, let us embrace the power of a² + b² and embark on a quest for deeper insights and understanding in the ever-expanding universe of mathematics.














